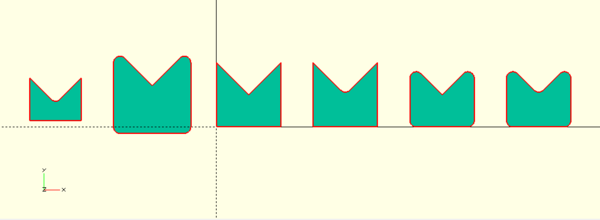A note on licensing
All code snippets shown on this page are intended to be used freely without any attribution and for any purpose, e.g. consider any code contribution here to be placed under Public Domain or CC0 license. This is not meant to change the normal license of the page as a whole and/or the manual itself.
Data
Map values from a list
// The function that maps input values x to output values, the // example uses floor() to convert floating point to integer // values. function map(x) = floor(x); input = [58.9339, 22.9263, 19.2073, 17.8002, 40.4922, 19.7331, 38.9541, 28.9327, 18.2059, 75.5965]; // Use a list comprehension expression to call the map() function // for every value of the input list and put the result of the // function in the output list. output = [ for (x = input) map(x) ]; echo(output); // ECHO: [58, 22, 19, 17, 40, 19, 38, 28, 18, 75]
Filter values in a list
// The function that define if the input value x should be // included in the filtered list, the example selects // all even values that are greater than 6. function condition(x) = (x >= 6) && (x % 2 == 0); input = [3, 3.3, 4, 4.1, 4.8, 5, 6, 6.3, 7, 8]; // Use a list comprehension expression to call the condition() // function for every value of the input list and put the value // in the output list if the function returns true. output = [ for (x = input) if (condition(x)) x ]; echo(output); // ECHO: [6, 8]
Add all values in a list
// Create a simple recursive function that adds the values of a list of floats;
// the simple tail recursive structure makes it possible to
// internally handle the calculation as loop, preventing a
// stack overflow.
function add(v, i = 0, r = 0) = i < len(v) ? add(v, i + 1, r + v[i]) : r;
input = [2, 3, 5, 8, 10, 12];
output = add(input);
echo(output);
// ECHO: 40
//------------------ add2 -----------------------
// An even simpler non recursive code version of add explores the
// the matrix product operator
function add2(v) = [for(p=v) 1]*v;
echo(add2(input));
// ECHO: 40
// add2 works also with lists of vectors
input2 = [ [2, 3] , [5, 8] , [10, 12] ];
echo(add2(input2));
// ECHO: [17, 23]
echo(add(input2));
// ECHO: undef // Why?
//----------------- add3 --------------------------
// With a little more code, the function add may be used also
// to add any homogeneous list structure of floats
function add3(v, i = 0, r) =
i < len(v) ?
i == 0 ?
add3(v, 1, v[0]) :
add3(v, i + 1, r + v[i]) :
r;
input3 = [ [[1], 1] , [[1], 2] , [[1], 3] ];
input4 = [ 10, [[1], 1] , [[1], 2] , [[1], 3] ];
echo(add3(input3));
// ECHO: [[3], 6]
echo(add2(input3));
// ECHO: undef // input3 is not a list of vectors
echo(add3(input4));
// ECHO: undef // input4 is not a homogeneous list
Cumulative sum
[Note: Requires version 2019.05]
//create a recursive cumulative-sum function using a c-style generator values = [1,2,65,1,4]; cumsum = [ for (a=0, b=values[0]; a < len(values); a= a+1, b=b+values[a]) b]; echo(cumsum); // ECHO: [1, 3, 68, 69, 73]
Count values in a list matching a condition
// The function that define if the input value x should be // included in the filtered list, the example selects // all even values that are greater than 6. function condition(x) = (x >= 6) && (x % 2 == 0); input = [3, 3.3, 4, 4.1, 4.8, 5, 6, 6.3, 7, 8]; // Use a list comprehension expression to call the condition() // function for every value of the input list and put the value // in the output list if the function returns true. // Finally the count is determined simply by using len() on the // filtered list. output = len([ for (x = input) if (condition(x)) x ]); echo(output); // ECHO: 2
Find the index of the maximum value in a list
// Create a function that find the index of the maximum value // found in the input list of floats function index_max(l) = search(max(l), l)[0]; input = [ 6.3, 4, 4.1, 8, 7, 3, 3.3, 4.8, 5, 6]; echo(index_max(input)); // Check it echo(input[index_max(input)] == max(input)); // ECHO: 3 // ECHO: true
Caring about undef
Most illegal operations in OpenSCAD return undef. Some return nan. However, the program keeps running and undef values may cause unpredictable future behaviour if no precaution is taken. When a function argument is missing in a function call, an undef value is assigned to it in evaluating the function expression. To avoid this, a default value may be assigned to optional function arguments.
// add 'a' to each element of list 'L' function incrementBy(L, a) = [ for(x=L) x+a ]; //add 'a' to each element of list 'L'; 'a' default is 1 when missing function incrementByWithDefault(L, a=1) = [ for(x=L) x+a ]; echo(incrementBy= incrementBy([1,2,3],2)); echo(incrementByWithDefault= incrementByWithDefault([1,2,3],2)); echo(incrementBy= incrementBy([1,2,3])); echo(incrementByWithDefault= incrementByWithDefault([1,2,3])); // ECHO: incrementBy= [3, 4, 5] // ECHO: incrementByWithDefault= [3, 4, 5] // ECHO: incrementBy= [undef, undef, undef] // ECHO: incrementByWithDefault= [2, 3, 4]
Sometimes the default value depends on other parameters of the call and cannot be set as before; a conditional expression solve this:
// find the sublist of 'list' with indices from 'from' to 'to'
function sublist(list, from=0, to) =
let( end = (to==undef ? len(list)-1 : to) )
[ for(i=[from:end]) list[i] ];
echo(s0= sublist(["a", "b", "c", "d"]) ); // from = 0, end = 3
echo(s1= sublist(["a", "b", "c", "d"], 1, 2) ); // from = 1, end = 2
echo(s2= sublist(["a", "b", "c", "d"], 1)); // from = 1, end = 3
echo(s3= sublist(["a", "b", "c", "d"], to=2) ); // from = 0, end = 2
// ECHO: s0 = ["a", "b", "c", "d"]
// ECHO: s1 = ["b", "c"]
// ECHO: s2 = ["b", "c", "d"]
// ECHO: s3 = ["a", "b", "c"]
The function sublist() returns undesirable values when from > to and generates a warning (try it!). A simple solution would be to return the empty list [] in this case:
// returns an empty list when 'from > to'
function sublist2(list, from=0, to) =
from<=to ?
let( end = (to==undef ? len(list)-1 : to) )
[ for(i=[from:end]) list[i] ] :
[];
echo(s1= sublist2(["a", "b", "c", "d"], 3, 1));
echo(s2= sublist2(["a", "b", "c", "d"], 1));
echo(s3= sublist2(["a", "b", "c", "d"], to=2));
// ECHO: s1 = []
// ECHO: s2 = []
// ECHO: s3 = ["a", "b", "c"]
The output s2 above is the empty list because to==undef and the comparison of from and to evaluates as false: the default value of to has been lost.
To overcome this it is enough to invert the test:
function sublist3(list, from=0, to) =
from>to ?
[] :
let( end = to==undef ? len(list)-1 : to )
[ for(i=[from:end]) list[i] ] ;
echo(s1=sublist3(["a", "b", "c", "d"], 3, 1));
echo(s2=sublist3(["a", "b", "c", "d"], 1));
echo(s3=sublist3(["a", "b", "c", "d"], to=2));
// ECHO: s1 = []
// ECHO: s2 = ["b", "c", "d"]
// ECHO: s3 = ["a", "b", "c"]
Now, when to is undefined, the first test evaluates as false and the let() is executed. With careful choices of tests, we can deal with undef values.
Geometry
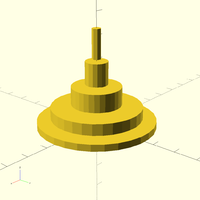
Stack cylinders on top of each other
// Define the sizes for the cylinders, first value is the
// radius, the second is the height.
// All cylinders are to be stacked above each other (with
// an additional spacing of 1 unit).
sizes = [ [ 26, 3 ], [ 20, 5 ], [ 11, 8 ], [ 5, 10 ], [ 2, 13 ] ];
// One option to solve this is by using a recursive module
// that creates a new translated coordinate system before
// going into the next level.
module translated_cylinder(size_vector, idx = 0) {
if (idx < len(size_vector)) {
radius = size_vector[idx][0];
height = size_vector[idx][1];
// Create the cylinder for the current level.
cylinder(r = radius, h = height);
// Recursive call generating the next cylinders
// translated in Z direction based on the height
// of the current cylinder
translate([0, 0, height + 1]) {
translated_cylinder(size_vector, idx + 1);
}
}
}
// Call the module to create the stacked cylinders.
translated_cylinder(sizes);
Minimum rotation problem
In 2D, except in very special cases, there are only two rotations that make a vector to align to another one. In 3D, there are infinitely many. Only one, however, has the minimum rotation angle. The following function builds the matrix for that minimum rotation. The code is a simplification of a function found in the Oskar Linde's sweep.scad.
// Find the unitary vector with direction v. Fails if v=[0,0,0].
function unit(v) = norm(v)>0 ? v/norm(v) : undef;
// Find the transpose of a rectangular matrix
function transpose(m) = // m is any rectangular matrix of objects
[ for(j=[0:len(m[0])-1]) [ for(i=[0:len(m)-1]) m[i][j] ] ];
// The identity matrix with dimension n
function identity(n) = [for(i=[0:n-1]) [for(j=[0:n-1]) i==j ? 1 : 0] ];
// computes the rotation with minimum angle that brings a to b
// the code fails if a and b are opposed to each other
function rotate_from_to(a,b) =
let( axis = unit(cross(a,b)) )
axis*axis >= 0.99 ?
transpose([unit(b), axis, cross(axis, unit(b))]) *
[unit(a), axis, cross(axis, unit(a))] :
identity(3);
Drawing "lines" in OpenSCAD
// An application of the minimum rotation
// Given to points p0 and p1, draw a thin cylinder with its
// bases at p0 and p1
module line(p0, p1, diameter=1) {
v = p1-p0;
translate(p0)
// rotate the cylinder so its z axis is brought to direction v
multmatrix(rotate_from_to([0,0,1],v))
cylinder(d=diameter, h=norm(v), $fn=4);
}
// Generate the polygonal points for the knot path
knot = [ for(i=[0:2:360])
[ (19*cos(3*i) + 40)*cos(2*i),
(19*cos(3*i) + 40)*sin(2*i),
19*sin(3*i) ] ];
// Draw the polygonal a segment at a time
for(i=[1:len(knot)-1])
line(knot[i-1], knot[i], diameter=5);
// Line drawings with this function is usually excruciatingly lengthy to render
// Use it just in preview mode to debug geometry
Another approach to the module line() is found in Rotation rule help.
Fit text into a given area
There is currently no way to query the size of the geometry generated by text(). Depending on the model it might be possible to calculate a rough estimate of the text size and fit the text into the known area. This works using resize() with the assumption the length is the dominating value.
// Generate 2 random values between 10 and 30
r = rands(10, 30, 2);
// Calculate width and length from random values
width = r[1];
length = 3 * r[0];
difference() {
// Create border
linear_extrude(2, center = true)
square([length + 4, width + 4], center = true);
// Cut the area for the text
linear_extrude(2)
square([length + 2, width + 2], center = true);
// Fit the text into the area based on the length
color("green")
linear_extrude(1.5, center = true, convexity = 4)
resize([length, 0], auto = true)
text("Text goes here!", valign = "center", halign = "center");
}
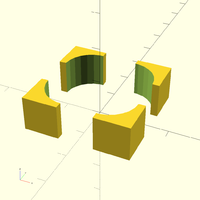
Create a mirrored object while retaining the original
The mirror() module just transforms the existing object, so it can't be used to generate symmetrical objects. However using the children() module, it's easily possible define a new module mirror_copy() that generates the mirrored object in addition to the original one.
// A custom mirror module that retains the original
// object in addition to the mirrored one.
module mirror_copy(v = [1, 0, 0]) {
children();
mirror(v) children();
}
// Define example object.
module object() {
translate([5, 5, 0]) {
difference() {
cube(10);
cylinder(r = 8, h = 30, center = true);
}
}
}
// Call mirror_copy twice, once using the default to
// create a duplicate mirrored on X axis and
// then mirror again on Y axis.
mirror_copy([0, 1, 0])
mirror_copy()
object();
Arrange parts on a spatial array
An operator to display a set of objects on an array.
// Arrange its children in a regular rectangular array
// spacing - the space between children origins
// n - the number of children along x axis
module arrange(spacing=50, n=5) {
nparts = $children;
for(i=[0:1:n-1], j=[0:nparts/n])
if (i+n*j < nparts)
translate([spacing*(i+1), spacing*j, 0])
children(i+n*j);
}
arrange(spacing=30,n=3) {
sphere(r=20,$fn=8);
sphere(r=20,$fn=10);
cube(30,center=true);
sphere(r=20,$fn=14);
sphere(r=20,$fn=16);
sphere(r=20,$fn=18);
cylinder(r=15,h=30);
sphere(r=20,$fn=22);
}
A handy operator to display a lot of parts of a project downloaded from Thingiverse.
Note: the following usage fails:
arrange() for(i=[8:16]) sphere(15, $fn=i);
because the for statement do an implicit union of the inside objects creating only one child.
Rounding polygons
Polygons may be rounded by the offset operator in several forms.
p = [ [0,0], [10,0], [10,10], [5,5], [0,10]]; polygon(p); // round pointed vertices and enlarge translate([-15, 0]) offset(1,$fn=24) polygon(p); // round concavities and shrink translate([-30, 0]) offset(-1,$fn=24) polygon(p); // round concavities and preserve polygon dimensions translate([15, 0]) offset(-1,$fn=24) offset(1,$fn=24) polygon(p); // round pointed vertices and preserve polygon dimensions translate([30, 0]) offset(1,$fn=24) offset(-1,$fn=24) polygon(p); // round all vertices and preserve polygon dimensions translate([45, 0]) offset(-1,$fn=24) offset(1,$fn=24) offset(1,$fn=24) offset(-1,$fn=24) polygon(p);
Filleting objects
Filleting is the 3D counterpart of the rounding of polygons. There is no offset() operators for 3D objects, but it may be coded using minkowski operator.
render()
difference(){
offset_3d(2) offset_3d(-2) // exterior fillets
offset_3d(-4) offset_3d(4) // interior fillets
basic_model();
// hole without fillet
translate([0,0,10])
cylinder(r=18,h=50);
}
module basic_model(){
cylinder(r=25,h=55);
cube([80,80,10], center=true);
}
module offset_3d(r=1, size=1e12) {
n = $fn==undef ? 12: $fn;
if(r==0) children();
else
if( r>0 )
minkowski(){
children();
sphere(r, $fn=n);
}
else {
size2 = size*[1,1,1];
size1 = size2*0.99;
difference(){
cube(size2, center=true);
minkowski(){
difference(){
cube(size1, center=true);
children();
}
sphere(-r, $fn=n);
}
}
}
}
Note that this is a very time consuming process. The minkowski operator adds vertices to the model so each new offset_3d takes longer than the previous one.
Computing a bounding box
There is no way to get the bounding box limits of an object with OpenSCAD codes. However, it is possible to compute its bounding box volume. Its concept is simple: hull() the projection of the model on each axis (1D sets) and minkowski() them. As there is no way to define a 1D set in OpenSCAD, the projections are approximated by a stick whose length is the size of the projection.
module bbox() {
// a 3D approx. of the children projection on X axis
module xProjection()
translate([0,1/2,-1/2])
linear_extrude(1)
hull()
projection()
rotate([90,0,0])
linear_extrude(1)
projection() children();
// a bounding box with an offset of 1 in all axis
module bbx()
minkowski() {
xProjection() children(); // x axis
rotate(-90) // y axis
xProjection() rotate(90) children();
rotate([0,-90,0]) // z axis
xProjection() rotate([0,90,0]) children();
}
// offset children() (a cube) by -1 in all axis
module shrink()
intersection() {
translate([ 1, 1, 1]) children();
translate([-1,-1,-1]) children();
}
shrink() bbx() children();
}
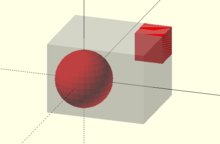
The image shows the (transparent) bounding box of a red model generated by the code:
module model()
color("red")
union() {
sphere(10);
translate([15,10,5]) cube(10);
}
model();
%bbox() model();
The cubes in the offset3D operator code of the Filleting objects tip could well be replaced by the object bounding box dispensing the artificial argument size.
As an example of solving problems with this, with a little manipulation of the result, the bounding box can be used to augment features around arbitrary text without knowing the size of the text. In this example a square base plate for the text is created with two holes inserted into it at the ends of the text, all having fixed margins. This works by taking the projection of the bounding box, expanding it evenly, shrinking the y dimension to a sliver, and extending the x direction outward by a sliver, and subtracting off the expanded bounding box projection again, leaving two near point-like objects which can be expanded with offset into the holes.
my_string = "Demo text";
module BasePlate(margin) {
minkowski() {
translate(-margin) square(2*margin);
projection() bbox() linear_extrude(1) children();
}
}
module TextThing() {
text(my_string, halign="center", valign="center");
}
hole_size = 3;
margwidth = 2;
linear_extrude(1)
difference() {
BasePlate([2*(hole_size+margwidth), margwidth]) TextThing();
offset(hole_size) {
difference() {
scale([1.001, 1])
resize([-1, 0.001])
BasePlate([hole_size+margwidth, margwidth]) TextThing();
BasePlate([hole_size+margwidth, margwidth]) TextThing();
}
}
}
linear_extrude(2) TextThing();
Data Heightmap
The builtin module surface() is able to create a 3D object that represents the heightmap of data in a matrix of numbers. However, the data matrix for surface() should be stored in an external text file. The following module does the exact heightmap of surface() for a data set generated by the user code.
data = [ for(a=[0:10:360])
[ for(b=[0:10:360])
cos(a-b)+4*sin(a+b)+(a+b)/40 ]
];
surfaceData(data, center=true);
cube();
// operate like the builtin module surface() but
// from a matrix of floats instead of a text file
module surfaceData(M, center=false, convexity=10){
n = len(M);
m = len(M[0]);
miz = min([for(Mi=M) min(Mi)]);
minz = miz<0? miz-1 : -1;
ctr = center ? [-(m-1)/2, -(n-1)/2, 0]: [0,0,0];
points = [ // original data points
for(i=[0:n-1])for(j=[0:m-1]) [j, i, M[i][j]] +ctr,
[ 0, 0, minz ] + ctr,
[ m-1, 0, minz ] + ctr,
[ m-1, n-1, minz ] + ctr,
[ 0, n-1, minz ] + ctr,
// additional interpolated points at the center of the quads
// the points bellow with `med` set to 0 are not used by faces
for(i=[0:n-1])for(j=[0:m-1])
let( med = i==n-1 || j==m-1 ? 0:
(M[i][j]+M[i+1][j]+M[i+1][j+1]+M[i][j+1])/4 )
[j+0.5, i+0.5, med] + ctr
];
faces = [ // faces connecting data points to interpolated ones
for(i=[0:n-2])
for(j=[i*m:i*m+m-2])
each [ [ j+1, j, j+n*m+4 ],
[ j, j+m, j+n*m+4 ],
[ j+m, j+m+1, j+n*m+4 ],
[ j+m+1, j+1, j+n*m+4 ] ] ,
// lateral and bottom faces
[ for(i=[0:m-1]) i, n*m+1, n*m ],
[ for(i=[m-1:-1:0]) -m+i+n*m, n*m+3, n*m+2 ],
[ for(i=[n-1:-1:0]) i*m, n*m, n*m+3 ],
[ for(i=[0:n-1]) i*m+m-1, n*m+2, n*m+1 ],
[n*m, n*m+1, n*m+2, n*m+3 ]
];
polyhedron(points, faces, convexity);
}
Strings
Integer from Numeric String (Decimal or Hex)
Converts number in string format to an integer, (s2d - String 2 Decimal - named before I added hex to it...)
e.g. echo(s2d("314159")/100000); // shows ECHO: 3.14159
function s2d(h="0",base=10,i=-1) =
// converts a string of hexa/or/decimal digits into a decimal
// integers only
(i == -1)
? s2d(h,base,i=len(h)-1)
: (i == 0)
? _chkBase(_d2n(h[0]),base)
: _chkBase(_d2n(h[i]),base) + base*s2d(h,base,i-1);
function _chkBase(n,b) =
(n>=b)
? (0/0) // 0/0=nan
: n;
function _d2n(digitStr) =
// SINGLE string Digit 2 Number, decimal (0-9) or hex (0-F) - upper or lower A-F
(digitStr == undef
|| len(digitStr) == undef
|| len(digitStr) != 1)
? (0/0) // 0/0 = nan
: _d2nV()[search(digitStr,_d2nV(),1,0)[0]][1];
function _d2nV()=
// Digit 2 Number Vector, use function instead of variable - no footprints
[ ["0",0],["1",1],["2",2],["3",3],["4",4],
["5",5],["6",6],["7",7],["8",8],["9",9],
["a",10],["b",11],["c",12],
["d",13],["e",14],["f",15],
["A",10],["B",11],["C",12],
["D",13],["E",14],["F",15]
];
Debug
Debug Tap function
Similar to Ruby's Tap function. This function encapsulates the echo to console side-effect, if $_debug is true and returns the object.
e.g. given $_debug is true; x = debugTap(2 * 2, "Solution is: "); // shows ECHO: Solution is: 4
function debugTap(o, s) = let(
nothing = [ for (i = [1:1]) if ($_debug) echo(str(s, ": ", o)) ]) o;
// usage
// note: parseArgsToString() just concats all the args and returns a pretty str
$_debug = true;
// doubles 'x'
function foo(x) =
let(
fnName = "foo",
args = [x]
)
debugTap(x * x, str(fnName, parseArgsToString(args)));
x = 2;
y = foo(x);
echo(str("x: ", x, " y: ", y));
// console display:
// ECHO: "foo(2): 4"
// ECHO: "x: 2 y: 4"